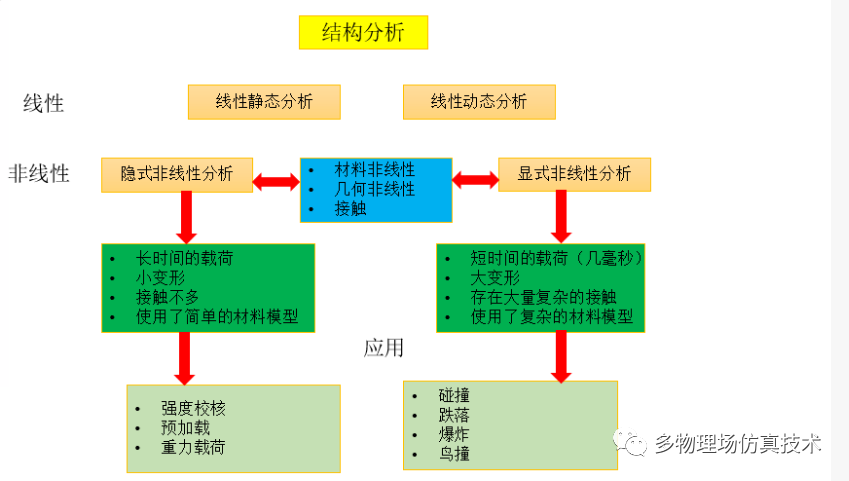
数据存储挑战
处理大模型时,数据组织形式和存储策略至关重要。例如,涉及一亿个实数自由度时,矩阵的大小可达到十的十六次方。若为稀疏矩阵,即便非零数据仅占全部数据的0.01%,其内存消耗也将达到八亿的十二次方,即8000吉字节。此外,在实际应用中,由于编译器配置、页面对齐以及硬件管理等众多因素,所需存储空间可能还会更多,这对存储资源构成了不小的压力。
处理如此庞大的数据量,若继续采用传统手段,既会消耗更多存储空间,又会提升费用。以大型工程模拟计算为例,这种数据规模和空间需求可能导致众多操作难以实施,因此,探索新的存储优化方法变得尤为关键。
const int NUMSIZE = 1e6;double value[NUMSIZE][NUMSIZE];
稀疏矩阵优化
const int NUMSIZE = 1e6;double **value;value = new double*[NUMSIZE];int i;for(i=0;i<NUMSIZE;i++){value[i]=new double[NUMSIZE];}
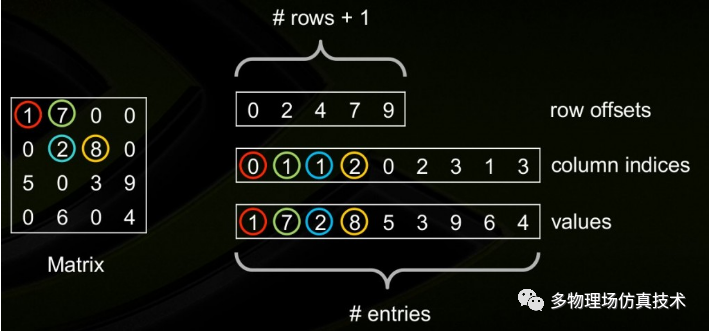
传统存储方式对稀疏矩阵来说既费空间又无必要。其实,有专门针对稀疏矩阵的优化存储方案,能显著降低空间占用。不少体验过矩阵求解库的用户都有体会,在处理过程中,矩阵的操作效率至关重要,而传统方法在这方面明显不够理想。
使用稀疏矩阵进行存储优化后,能有效降低空间损耗。同时,这种优化还能促进处理速度的提升。在科学计算中,这种高效的存储手段对于复杂模型的顺利处理至关重要,它有助于防止因存储空间不足而引发的计算中断,为后续的分析和计算提供了坚实的基础。
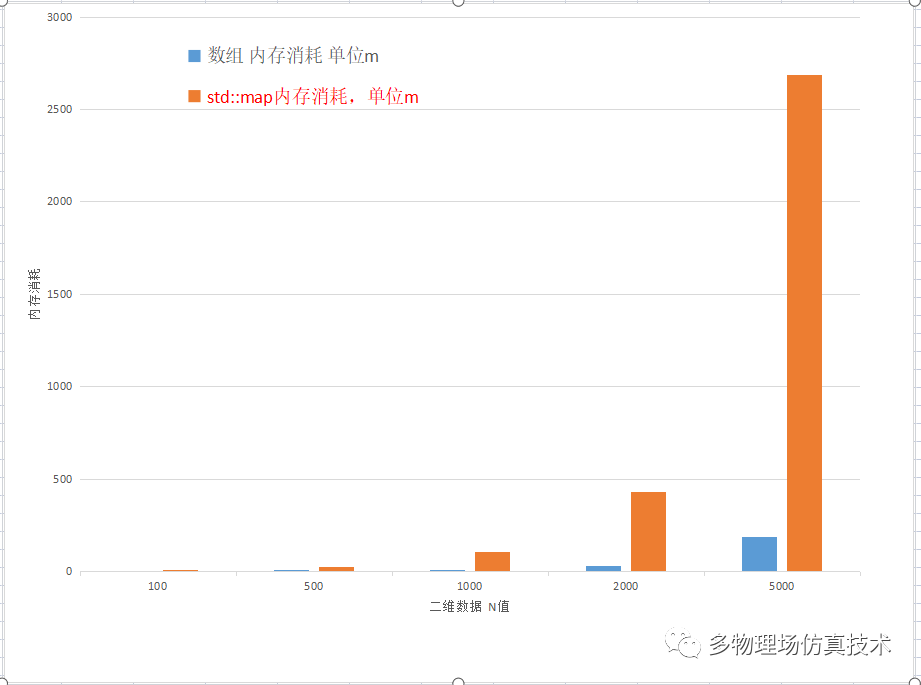
int x[NUMSIZE];int y[NUMSIZE];double value[NUMSIZE];
map<pair<int,int>,double> values;C++模板优势
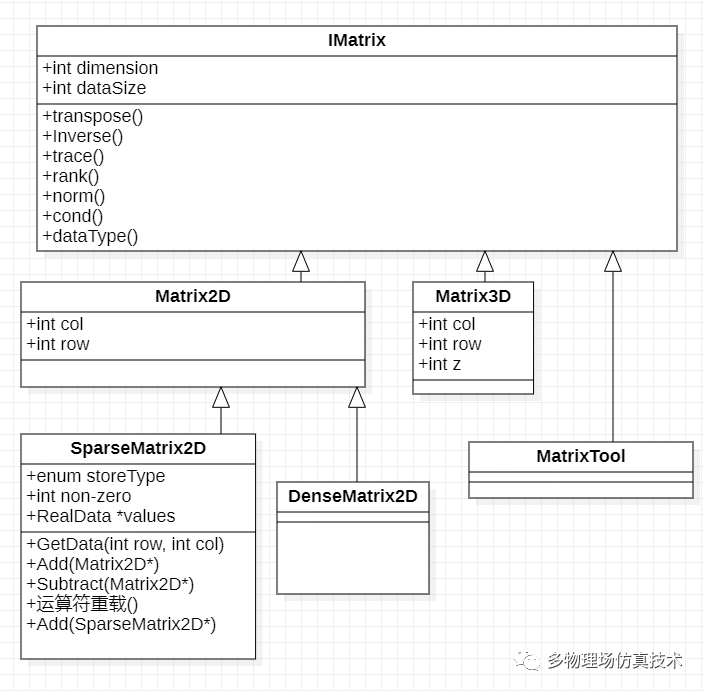
C++的模板特性非常突出。它能以统一的数据结构形式处理多种数据类型,例如浮点数和整数等。在矩阵的定义上,开发者可以充分利用这一特性,依据实际需求挑选恰当的数据类型。
这种特性显著增强了代码的可重复使用性,使得相同的代码框架得以在多个项目中应用,只需根据实际需要稍作调整。无论是简单的计算程序还是结构复杂的系统,C++的模板技术均能满足其矩阵处理需求,有力地促进了高效开发。
独立通用模块
在处理大型模型时,应确保模块独立且具备通用性。这类模块不与特定业务或算法绑定,能够根据外部输入参数进行灵活配置。由于不同物理场计算的刚度矩阵组装流程具有相似性,这为模块的通用化创造了条件。
在设计和开发求解器时,通用模块的应用能有效提升开发速度,降低重复工作。在众多物理场景的模拟计算任务中,借助这些模块,我们能够迅速构建处理框架,便于执行各类物理场的计算。
指令与并行计算
指令优化对于大型模型至关重要。为了适应特定硬件的指令支持,我们在编写程序时应当巧妙运用指令集,这样做能有效提升计算速度。有限元求解器主要处理的是矩阵,而处理大规模矩阵时,需要用到分块处理、矩阵分解以及并行计算等方法。
并行计算显著提升了计算速度,关键在于负载的合理分配。以稀疏矩阵与向量的乘法为例,其负载均衡问题可转化为图形的多路划分问题。在具体应用,比如大规模气象模拟时,必须保证每个计算资源都能被合理地分配到相应的计算任务中,防止硬件资源浪费,这样才能最大限度地发挥计算潜力。
计算流程模块化
对整个计算仿真流程进行模块化处理十分关键。根据功能的重要性进行分类,每个模块都通过文件形式提供接口。这样的模块可以单独展现整个模型的数据特性,例如网格质量评估、敏感性分析等。
大型模型与计算硬件关系密切,部分工具库需在运行机器上编译和优化。超大规模有限元模型的求解方式依赖于数据特性,并无统一的标准,需在实践探索适宜的方法。具体应用时,依据模型特性挑选恰当的求解策略,能提升计算精度与效率。
在使用大模型的过程中,大家是否遇到过特别棘手的存储和计算效率难题?别忘了点赞并转发这篇文章!