堆排序与中序遍历
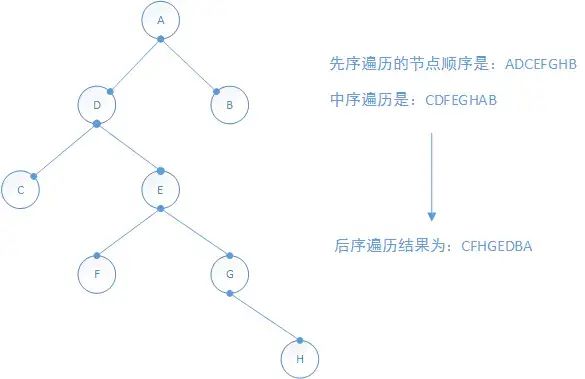
序列一开始是1、8、6、2、5、4、7、3,通过堆排序构建小根堆,小根堆的特点是每个节点的数值都小于其左右子节点。构建完成后,序列变为1、2、4、3、5、6、7、8。按照中序遍历的左根右顺序进行。堆排序在1964年被提出,这道题目的结果是8、3、2、5、1、6、4、7。它经常在数据结构考试中出现,理解它有助于更好地掌握树的遍历和排序方法。
堆排序在处理大量数据排序时表现出色。众多大型电商平台在排序大量商品时,常常运用这种原理。中序遍历可以清楚地呈现二叉树节点的排列顺序。在数据库索引结构的优化过程中,这种方法同样被广泛应用。掌握这些知识,对于从事算法领域的工作大有裨益。
函数返回值问题
当 n 等于 5 时,我们需要观察函数的输出。这涉及到集合之间的真包含关系,包括递归可枚举、上下文相关、上下文无关以及正规语言等类别。符号“#”在这里起到占位符的作用。例如,在题目中“# add(a+b) a+b”表示将“add(a+b)”替换为“a+b”,那么代码输出的结果将是“(%dn,5*3+4)”。因此,得出的结果 D 是正确的。这种题目在编程语言学习初期常遇到。
在编程语言的演进过程中,函数的编写和语法的应用持续得到优化。这类题目有助于检验对语言特性的理解,例如代码的替换机制。在编程实践中,诸如预处理指令等,也具备类似的替换功能。正确理解题目中 # 的含义,对于编写更复杂的程序至关重要。
网络开发基础题
[cpp] view plaincopy
int foo(int n)
{
if(n<2)return n;
return foo(n-1)+foo(n-2);
}
这道题目是基础性的,不论是哪种开发类型,都必然需要依赖网络。网络开发的核心在于 HTTP 协议,正确答案是 B。HTTP 协议自 1991 年问世以来,对互联网的发展起到了关键作用。它是数据传输的基础,网页浏览和文件下载等功能都建立在其之上。
如今,互联网应用广泛,众多网站和APP与服务器交流都依照HTTP协议。为确保服务器能准确回应请求,必须使用恰当的响应码。对于开发者来说,掌握HTTP协议是不可或缺的能力。不少初级开发者面试时都会遇到这类问题,这充分说明了其重要性。
( 3 * 0.01% ) / ( 3 * 0.01% + 5 * 0.015% ) = 28.6%进制问题分析
这是一道选择题,从选项A开始。假设使用6进制,等式15乘以4等于112,转换成十进制就是11乘以4等于44,等式成立,因此选择A。或者设定进制为X,且X要大于5,通过计算(x+5)乘以4等于x的平方加x加2,可以得到x等于6。进制转换是计算机基础课程中常提到的内容。
计算机内部数据的基本表示形式是二进制。本题需要确定进制。在早期的计算机设计阶段,就出现了多种进制。在密码学、数据存储等众多领域,进制转换和计算至关重要。例如,在数据加密过程中,通过改变数制来确保信息安全。
哈夫曼编码问题
文本字母出现频率分别为:a出现4次,b出现3次,o出现12次,h出现7次,i出现10次,这些频率数据被用于哈夫曼编码。我们设定A、B、C、D这四个字母的编码分别是00、01、10、11。根据这个编码,电文“100”由14位组成。译码时,我们按照每两位一组来恢复原文。在哈夫曼编码中,每个字母对应一个叶节点,通过比较频率,将频率最小的节点合并,形成新的节点。这种编码方法最早由哈夫曼在1952年提出。
数据压缩领域广泛采用哈夫曼编码。这种编码在图片和视频压缩中尤为常见,它有助于缩小存储空间和带宽。字母出现的频率会影响编码的长度。在多媒体文件传输过程中,恰当的编码能提升传输速度,节约资源,使用户能够更顺畅地接收信息。
#define add(a+b) a+b
int main()
{
printf(“%dn”,5*add(3+4));
return ;
}
栈的输出序列
栈的入栈顺序是A、B、C、D、E,根据选项C,元素a不可能先出栈。这是因为栈遵循后进先出的原则。在编程中,栈常被用于处理函数调用和表达式计算。操作系统在执行程序时,会利用栈来管理执行上下文。此外,编译器在语法分析过程中也会借助栈的功能。
明白栈的输出顺序规则有助于减少编程中的错误。这一知识点常被计算机考研和程序员面试所考察。递归函数的实现与栈机制紧密相连。错误的栈操作可能引发程序崩溃。精通栈的知识对于构建稳固的程序至关重要。
你对哪种算法选择题类型特别感兴趣?不妨给这篇文章点个赞,分享出去,并在评论区展开讨论。