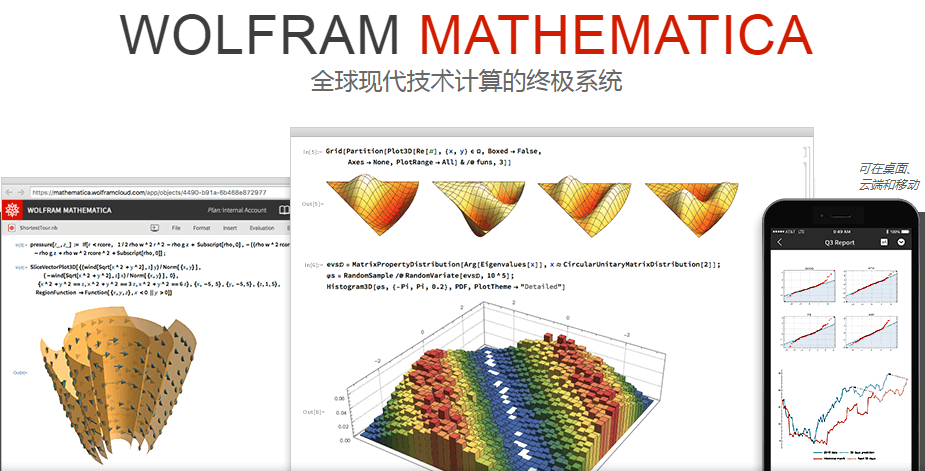
为了便于技术人员和学生等群体更便捷地完成技术运算,经过三十年精心研发的先进系统应运而生。该系统功能全面,操作简便,现已成为全球技术计算领域的佼佼者。接下来,我们将详细了解其强大之处。
先进技术引领
该系统经过三十年不懈研发,深耕技术计算领域,逐步形成了领先的技术体系。在这漫长的岁月里,众多科研工作者投入了心血,通过持续的研究和革新,其核心算法变得更加精确和高效。在全球各地,众多技术创新者利用它攻克了众多复杂的计算难题,为科技进步作出了重要贡献。
主要计算环境
这个环境是全球众多技术创新者、教育者和学子等人士的重要计算平台。在大学课堂中,教师用它向学生展示复杂的计算步骤;而在科研机构中,研究人员用它推进前沿技术的研究。成千上万的用户都依赖这个平台进行各自的技术计算。
二维形状生成
系统能够生成各式各样的平面图形。用户只需使用相应的指令,便可以轻松构建出所需的形状。众多几何图形都可通过输入一系列坐标值来定义,通过变换坐标组合,便可获得不同的平面图形。在实际操作过程中,无论是基础的矩形,还是结构复杂的多边形,都能迅速且精确地生成。
组合图形样式
用户可将参数与指令配合,以列表形式输入,实现图形的拼接与样式调整。通过此法,用户能将数个基础图形融合,形成复杂且风格独特的图形,并可根据实际需要调整色彩、线条粗细等细节。这就像玩积木,可以随意组合,满足各种设计需求。
生成与计算属性
通过特定指令,我们可以创建三角形。一旦生成,系统便能自动计算诸如面积等属性。用户只需输入图形的必要参数,系统便能快速给出精确答案。这样做既节省了时间,又提升了计算的精确度,使得用户无需亲自完成复杂的计算过程。
三维物体展示
系统能通过特定指令来呈现三维模型。这种展示方式让物体的三维结构一目了然,对学习工程制图、机械设计等专业的学生而言,极具实用性。此外,系统还能进行体积计算以及其他属性分析,为相关领域的研究与设计工作提供了强大助力。
自然语言输入
用户能够用日常语言来搜索公式及相关资料。这一特性显著简化了操作步骤,降低了使用难度。即便用户对专业指令不甚了解,也能借助自然语言轻松获取所需信息,其便捷程度如同与朋友交谈。
内置几何变换
系统自带了几何变换的功能,包括平移、旋转以及缩放等。这些功能让用户能够对图形进行多样化的操作,进而生成更多富有创意的图形。在平面设计和动画制作等众多领域,这些变换功能扮演着至关重要的角色。
卓越特性优势
该系统凭借其卓越的技术和简便的操作在全球范围内赢得了良好声誉。它提供了一个集成度高、持续升级的系统,其中包含了广泛而深入的技术计算功能。用户无需在多种软件间频繁切换,单一系统即可满足所有需求。此外,系统还支持通过网页浏览器进行云端访问,并在所有主流桌面系统上提供本地访问功能。
获取服务方式
系统有免费试用版可供使用。如需了解系统功能、试用详情或咨询教育版、政府版、商业版的购买事宜,请咨询在线客服。客服团队将提供详尽解答和协助,确保用户能更高效地使用系统。
你是否也急切地想要尝试这个功能强大的计算系统?快为这篇文章点赞、转发,让更多的人知道!